[Komentarz Kaczusia]
| Tym razem znowu pogrzebiemy w metodach numerycznych, jednak teraz nie dam wam do myślenia, lecz przedstawię jedną z najprostrzych metod numerycznych pozwalających znaleźć ekstrema (maksima i minima) funkcji. Najpierw opiszę jak znaleźć tą metodą minimum, a następnie, jak zmodyfikować program do poszukiwań maksimum takiej funkcji. |
|---|
Najpierw założenia; w sumie to jest tylko jedno, ale podstawowe - ciągłość funkcji na przedziale (czyli odpada funkcja f(x)=1/x na przedziale <-1, 1>).
Poza krańcami, potrzebujemy jeszcze dwóch punktów kontrolnych. Znajdujemy je korzystając z proporcji tzw. "złotego środka" - stąd nazwa metody - "metoda złotego podziału".
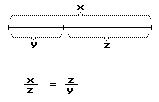
czyli długość całośc i ma się tak do długości dłuższego z odcinków, jak dłuższy odcinek do krótszego :) - ale wystarczy tych gierek słownych. Łatwo zauważyć, że do rozwiązania będzie równanie kwadratowe. Jednak rozwiązywanie za każdym razem takiego równania - to niepotrzebne liczenie. Można zauważyć, że dłuższy odcinek ma długość (w przybliżeniu) 0.618 całości, łatwo policzyć, że 0.382 całości to krótszy odcinek.
Gdy wyznaczymy już punkty pomocnicze - należy je teraz porównać i w zależności od ich wartości zawęzić przedział. Niech:
f(x) - funkcja, której minimum szukamy
<a, b> - przedział, na którym tego minimum szukamy
xa, xb - punkty pomocnicze
Jeśli f(xa)>f(xb), to przedział zawężamy do przedziału <xa,b> (na pierwszy rzut oka trochę nielogicznie, ale jak się zastanowić - to ma to sens). I tak postępujemy, aż odcinek poszukiwań będzie krótszy niż dokładność z jaką poszukujemy rozwiązania.
Jeden z nich wykonywany jest dokładnie jak w opisie - tzn. za każdym razem liczone są nowe punkty pomocnicze (program przykładowy również bazuje na tym algorytmie).
Drugi - bardziej popularny ze względu na mniej wykonywanych obliczeń - bazuje na tym, że liczymy tylko jeden punkt kontrolny - ze strony z której zawęziliśmy przedział; jak łatwo zauważyć zwiększy nam to ilość iteracji, eliminując jednocześnie jedno mnożenie zmiennoprzecinkowe. Na wynik jednak nie będzie miało to wpływu - różnica otrzymanych wyników nie przekroczy dokładności z jaką szukaliśmy miejsca zerowego.
Zaletą tej metody jest tak zwana "dobra zbieżność" (czyli, że jeśli tylko funkcja jest ciągła, to miejsce ekstremalne na pewno znajdziemy). Wadą jest "wolna zbieżność" metody (czyli, że obliczenia trwają długo) - wolno, ale konsekwentnie dążymy do rozwiązania problemu, czyli znalezienia wartości minimalnej funkcji na wybranym przedziale.
Oczywiście obiecałem powiedzieć, jak napisać również funkcję szukającą maksimum danej funkcji. Przecież to proste - powiecie, wystarczy skopiować funkcję liczącą minimum, zmienić jej nazwę i znaki przy porównaniach i po kłopocie. Tylko po co wydłużać niepotrzebnie program, przecież jeśli policzycie minimum funkcji g(x)=-f(x), to znajdziecia maksimum funkcji f(x) :)) (proste prawda?). Jeśli mi nie wierzycie - narysujcie sobie jakąkolwiek funkcję, a następnie tą funkcję przemnóżcie przez -1 i narysujcie wykres tak otrzymanej funkcji - zaręczam Wam, że będzie to lustrzane odbicie funkcji pierwotnej (no chyba, że ręka wam zadrży i krzywo narysujecie :)).
int Min = 1; // flaga oznaczająca minimalizowanie funkcji - jeśli 0
// maksymalizujemy funkcję, w przeciwnym wypadku maksymalizujemy
double F(double x)
// funkcja - zwraca wartość funkcji matematycznej w punkcie x
{
if(Min)
return wzór_funkcji;
else
return -1*wzór_funkcji;
}
lub jeśli wykorzystamy opisywaną bibliotekę fclass do pobrania wzoru funkcji:
int Min = 1;
double F(Func *f,x)
{
if(Min)
return f->eval(x);
else
return -1*(f->eval(x));
}
No i na zakończenie tradycyjnie parę słów na temat dołączonego listingu. Proszę się nie przerażać zapisami typu
#include <iostream.h>
myślałem, aby to zmienić, ale z drugiej strony to archiwum tego jak to wyglądało w latach 90.
Na tym kończę, życząc przyjemnej zabawy. Zainteresowanych innymi artykułami o programowaniu zapraszam na stronę Drobne Programowanie.
Kaczuś/BlaBla