Całkowanie metodami numerycznymi
[Komentarz LeMUra]
[Komentarz Kaczusia]
W skrócie
|
Jakiś czas temu w MA pojawił się artykuł na temat całkowania metodami numerycznymi. Ja na łamach
Izviestii chciałbym kontynuować rozpoczęty tam temat. Mam nadzieję, iż czytający ten tekst zapoznali
się z tamtym artykułem (MA 8/95), jeżeli nie to i tak zapraszam do zapoznania się z problemem.
|
W artykule z Magazynu Amiga było opisane jak metodą trapezów, oraz
najmniejszych kwadratów znaleźć całkę oznaczoną na pewnym przedziale (czyli
pole powierzchni zawarte między wykresem funkcji, a osią 0X). Ja natomiast
chciałbym pójść dalej i pokazać wam jak policzyć całę podwójną funkcji dwóch
zmiennych, czyli objętość zawartą między wykresem funkcji i płaszczyzną
wyznaczoną przez osie XY (qrcze, tu już pewnie niektórych przechodzą ciarki, a
co dopiero jak ja chcę jeszcze ograniczyć boki tak powstałej figury
funkcjami...). Ale nie przejmujcie się nie jest to takie trudne na jakie
wygląda :))), a jeśli komuś nie uda się tego złapać po pierwszym przeczytaniu
proponuję najpierw przejrzenie przykładu, a następnie powtórną lekturę
artykułu.
Tak więc nawiązując do artykułu z MA również podzielimy naszą figurę na
kilka (no może trochę więcej niż kilka :) mniejszych figur. Będą to ciękie, ale
długie wielościany (przede wszystkim graniastostosłupy, ale o tym później).
Policzymy objętości tych figur i zsumujemy je (czyli dla wtajemniczonych nie
mniej ni więcej, tylko korzystanie z definicji całki Riemmana (hi Elis - może
kiedyś znowu podyskutujemy sobie w języku zrozumiałym dla nielicznych? :)).
Czyli jak widać nic trudnego do zakodowania, mógłbym na tym skończyć mój
artykuł, ale sądzę, iż powinienem wyczulić czytających na kilka istotnych
rzeczy.
Pierwszą dość istotną rzeczą jest podział powierzchni X0Y na małe wielokąty
(przede wszystkim prostokąty) Jak to zrobić? Należy sobie ustalić szerokość
podziałki zarówno na osi X, jak i Y. Jeżeli naszą płaszczyznę mielibyśmy
ograniczoną prostokątem nie byłoby problemu. Po prostu dzielimy na małe
prostokąciki i po kłopocie. Sprawa natomiast komplikuje się gdy z góry i z dołu
ograniczamy funkcjami. 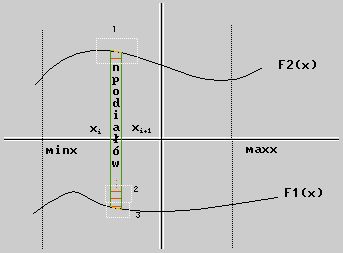 Najprościej byłoby ustalić ilość podziałów i po
kłopocie, ale czy na pewno? Mamy wtedy problem ze zmienną dokładnością
obliczeń, co przy niektórych funkcjach może doprowadzić do naprawdę dziwnych
wyników. Proponuję więc podział na równe prostokąty (metoda najmniejszych
kwadratów; dobrze - ktoś powie, ale wtedy może się okazać, iż pomijamy dość
duże fragmenty funkcji... Niekoniecznie, ponieważ połączymy tą metodę z metodą
trapezów (cóż matematyka to taka dziedzina, że trudno jest nam znaleźć
najlepszą i uniwersalną metodę, która byłaby odporna na różne "przypadłości",
dlatego nie należy ograniczać swojej wiedzy jedynie do jednej czy dwu metod -
zawsze na problem należy spojrzeć ogólniej, poznać wszystkie za i przeciw
metody, oraz dobrać tak zestaw metod, aby w miarę możliwości się uzupełniały).
To znaczy cały środek dzielimy na równe małe prostokąty
Najprościej byłoby ustalić ilość podziałów i po
kłopocie, ale czy na pewno? Mamy wtedy problem ze zmienną dokładnością
obliczeń, co przy niektórych funkcjach może doprowadzić do naprawdę dziwnych
wyników. Proponuję więc podział na równe prostokąty (metoda najmniejszych
kwadratów; dobrze - ktoś powie, ale wtedy może się okazać, iż pomijamy dość
duże fragmenty funkcji... Niekoniecznie, ponieważ połączymy tą metodę z metodą
trapezów (cóż matematyka to taka dziedzina, że trudno jest nam znaleźć
najlepszą i uniwersalną metodę, która byłaby odporna na różne "przypadłości",
dlatego nie należy ograniczać swojej wiedzy jedynie do jednej czy dwu metod -
zawsze na problem należy spojrzeć ogólniej, poznać wszystkie za i przeciw
metody, oraz dobrać tak zestaw metod, aby w miarę możliwości się uzupełniały).
To znaczy cały środek dzielimy na równe małe prostokąty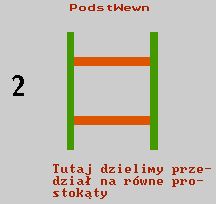 , natomiast pozostałości
dzielimy na trapezy
, natomiast pozostałości
dzielimy na trapezy  i trójkąty (trapez ze zdegerowaną do zera podstawą krótszą
:).
i trójkąty (trapez ze zdegerowaną do zera podstawą krótszą
:).
OK mamy już podział, teraz definicja całki Riemmana mówi nam o tym, iż
należy z takiego obszaru wybrać punkt reprezentujący ten obszar. Najłatwiej
byłoby wybrać któryś z wierzchołków prostokąta (trapezu, lub trójkąta), lecz
wtedy dostalibyśmy wynik dość nieprecyzyjny ale przede wszystkim zamazujący
informacje o funkcji. W takim razie, jak mówi nam doświadczenie najlepsze są
wartości środkowe, ale musimy wtedy wyznaczać punkty leżące w środku danego
obszaru, a w przypadku trójkąta i trapezu nie jest to najprostrze. Co nam zatem
pozostaje? Wartość średnia! Do średniej będziemy brać wartości funkcji we
wszystkich wierzchołkach (w trójkącie 3, w prostokącie 4, w trapezie 5) więc
ostateczny wzór stosowany do metody, to suma licz policzonych ze wzoru:
s[i] = P[i] * Ws[i];
gdzie:
s[i] - i-ty element sumy
P[i] - pole kolejnego małego obszaru (trójkąta, prostokąta lub trapezu)
Ws[i] - wartość średnia policzona na wierzchołkach tej figury
Kolejna uwaga, to fakt, iż należy uważać jeszcze na błąd zaokrąglenia na małe
odcinki, ponieważ może okazać się, iż po takim podziale w wyniku zaokrąglenia
dodając do siebie kolejne fragmenty odcinka przy ostatnik kroku znajdziemy się
po za przedziałem w którym liczymy. Jeżeli funkcja ta jest ciągła poza tym
przedziałem, a przynajmniej określona, to błąd obliczeń będzie niewielki, ale
gdy funkcja nie jest określona poza przedziałem to mogą dziać się dziwne
rzeczy. Dlatego (nie wiem, czym dokładnie jest ten błąd spowodowany i czy
występuje on również na Amidze, podejrzewam, iż jest to wina bibliotek
matematycznych) [problem leży po stronie reprezentacji liczb zmiennoprzecinkowych
na maszynach liczących],
zamiast pisać:
for(i=0; warunek; i++)
{
poczatek = koniec;
koniec += podzial;
}
piszemy:
for(i=0; warunek; i++)
{
poczatek = koniec;
koniec = zero + (i+1)*podzial;
}
gdzie:
i - licznik,
warunek - warunek, dopóki ma być wykonywana pętla,
poczatek - początek kolejnego przedziału,
koniec - koniec kolejnego podziału,
podzial - długość podziału odcinka,
zero - początek pierwszego przedziału
Uwagi do listingu
- spr
- Funkcja sprawdza, czy wprowadzanedo niej liczby (argumenty) są
wprowadzane rosnąco, jeśli nie - funkcja zmienia ich kolejność
- Max
- funkcja zwraca wartość większego z wprowadzonych argumentów
- Min
- funkcja zwraca wartość mniejszego z wprowadzonych argumentów
- PodstWew
- funkcja liczy pole podstawy figury 'wewnętrznej' (rysunek)
- PodstZew i PodstZew2
- funkcje liczące pole podstawy figury 'zewnętrznej'
- Funkcja
- funkcja zwraca wartość całkowanej funkcji
- F1, F2
- funkcje zwracające wartości funkcji ograniczających
- Calka
- funkcja liczy objętość pola pod wykresem funkcji całkowanej
ograniczonej płaszczyzną OXY oraz powierzchniami prostopadłymi do tej
płaszczyzny przechodzące przez wykresy odpowiednich funkcji x=xmin, x=xmax,
y=F1, y=F2
W programie zostały użyte funkcje specyficzne dla języka C, przykładem może
być operator ?:, zamiast niego mógłbym oczywiście użyć kilku innych funkcji i
efekt byłby ten sam, ale w celach edukacyjnych, jak również dla skrócenia kodu
programu użyłem tego operatora. Winny jestem zatem małe wyjaśnienie, otóż
składnia tej funkcji (bo jak by nie było, to operator jest funkcją, tyle że
możemy ją inaczej - w bardziej obrazowy sposób wywołać - o tym możecie się
dowiedzieć w 3 części kursu programowania obiektowego prowadzonego również
przeze mnie ;).
warunek ? wartość1 : wartość2;
- warunek
- wyrażenie, które w zależności od tego, czy jest równe 0, czy też nie
zwraca różne wartości - wartość1, lub wartość2.
Zamiast tego moglibyśmy
zapisać:
if(warunek)
return wartość2;
else
return wartość1;
czyli aż 4 linijki - a tak piszemy tylko 1 i efekt jest ten sam :))
Mimo, iż nie używałem ani funkcji, ani bibliotek z C++, to jednak listing
jest jako cpp - nie powinno to mieć wpływu na zrozumienie, po prostu
archaicznie napisany kompilator czepia się w miejscach gdzie błędów nie ma
(przynajmniej według standartu ANSI C), natomiast nie zauważa ich kompilując
całość jako cpp. Takie obejście problemu - po prostu nie lubię użerać się z
kiepskimi kompilatorami.
Aha, zapomniałbym, niestety przy zbyt dużej dokładności obliczeń mamy troszkę
czekania, np. gdy zwiększyłem dokładność 10 krotnie (0.001 i 2000 podziałów) u
mnie obliczenia trwały około godziny (030 - 50MHZ)
Kaczuś
.
Listing jako Bonus stuff.
Powrót do Menu
 Najprościej byłoby ustalić ilość podziałów i po
kłopocie, ale czy na pewno? Mamy wtedy problem ze zmienną dokładnością
obliczeń, co przy niektórych funkcjach może doprowadzić do naprawdę dziwnych
wyników. Proponuję więc podział na równe prostokąty (metoda najmniejszych
kwadratów; dobrze - ktoś powie, ale wtedy może się okazać, iż pomijamy dość
duże fragmenty funkcji... Niekoniecznie, ponieważ połączymy tą metodę z metodą
trapezów (cóż matematyka to taka dziedzina, że trudno jest nam znaleźć
najlepszą i uniwersalną metodę, która byłaby odporna na różne "przypadłości",
dlatego nie należy ograniczać swojej wiedzy jedynie do jednej czy dwu metod -
zawsze na problem należy spojrzeć ogólniej, poznać wszystkie za i przeciw
metody, oraz dobrać tak zestaw metod, aby w miarę możliwości się uzupełniały).
To znaczy cały środek dzielimy na równe małe prostokąty
Najprościej byłoby ustalić ilość podziałów i po
kłopocie, ale czy na pewno? Mamy wtedy problem ze zmienną dokładnością
obliczeń, co przy niektórych funkcjach może doprowadzić do naprawdę dziwnych
wyników. Proponuję więc podział na równe prostokąty (metoda najmniejszych
kwadratów; dobrze - ktoś powie, ale wtedy może się okazać, iż pomijamy dość
duże fragmenty funkcji... Niekoniecznie, ponieważ połączymy tą metodę z metodą
trapezów (cóż matematyka to taka dziedzina, że trudno jest nam znaleźć
najlepszą i uniwersalną metodę, która byłaby odporna na różne "przypadłości",
dlatego nie należy ograniczać swojej wiedzy jedynie do jednej czy dwu metod -
zawsze na problem należy spojrzeć ogólniej, poznać wszystkie za i przeciw
metody, oraz dobrać tak zestaw metod, aby w miarę możliwości się uzupełniały).
To znaczy cały środek dzielimy na równe małe prostokąty , natomiast pozostałości
dzielimy na trapezy
, natomiast pozostałości
dzielimy na trapezy  i trójkąty (trapez ze zdegerowaną do zera podstawą krótszą
:).
i trójkąty (trapez ze zdegerowaną do zera podstawą krótszą
:).